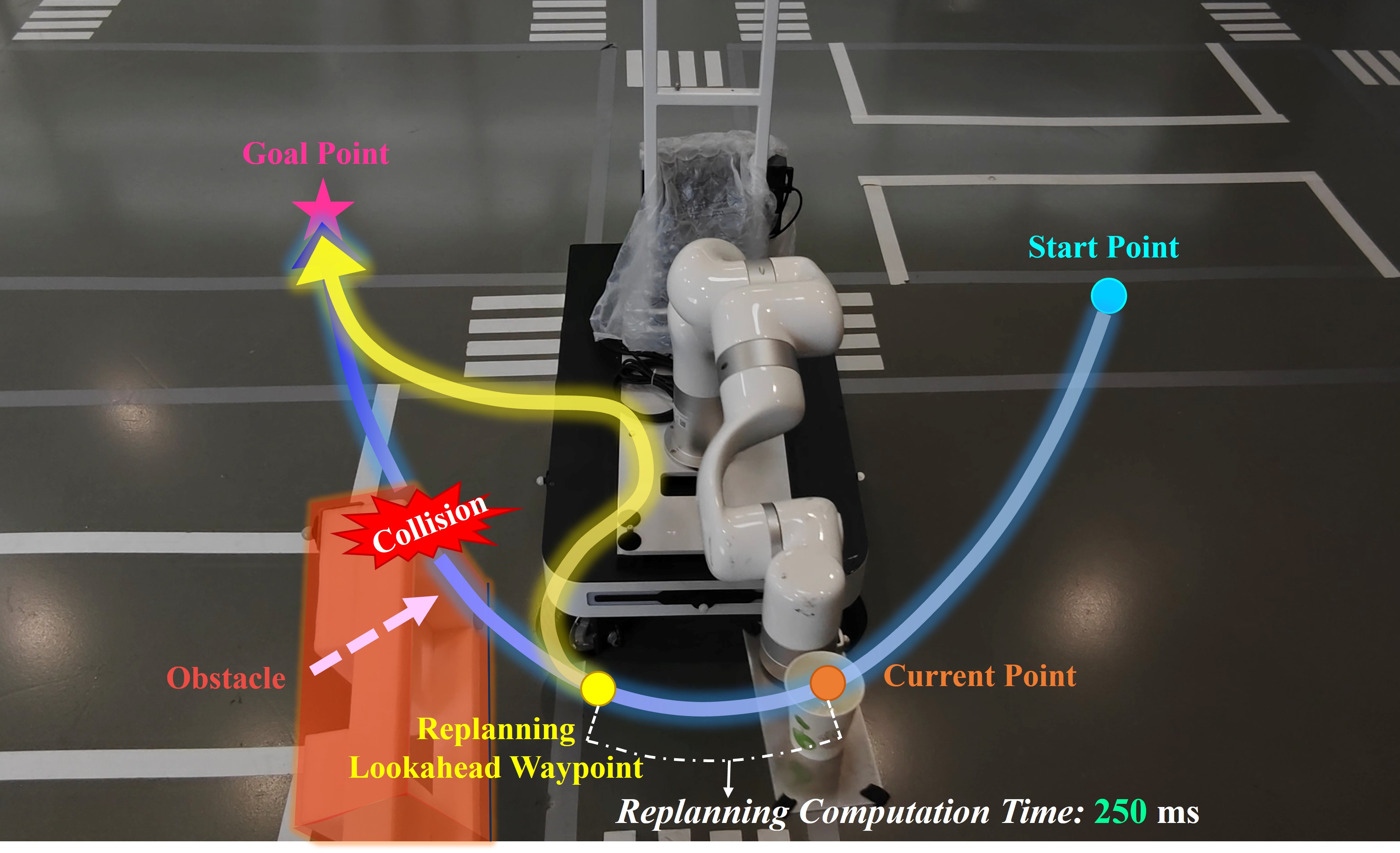
Non-prehensile transportation holds significant promise for robotic service applications. However, existing methods often fail to reconcile global navigability in complex scenarios with local reactivity. To bridge this gap, this letter proposes a reactive motion planning framework for non-prehensile transportation using robotic arms in cluttered environments. To adapt to environmental changes, the framework employs a proactive, periodic replanning strategy coupled with a passive, time-to-collision (TTC)-triggered safety mechanism. Both components are underpinned by a hierarchical trajectory generator that utilizes a constrained path planner to provide global geometric guidance for circumventing local minima, followed by a two-stage optimization process. In particular, to enhance computational efficiency, the optimization process incorporates soft penalty terms rather than hard constraints to refine trajectories and promote contact stability throughout the motion. Baseline comparisons validate the navigation advantages of the proposed method, while extensive experiments further characterize the performance boundaries and applicability of this soft-constraint formulation.
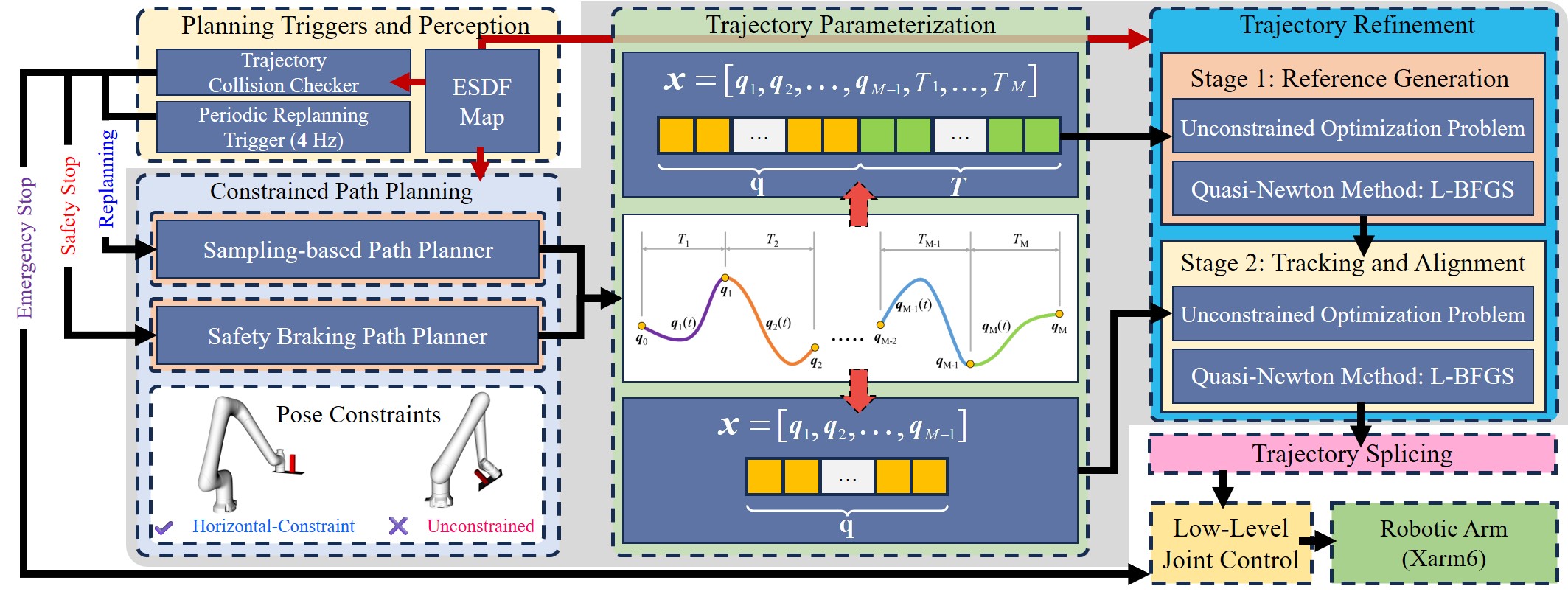
Fig. 2. Risk-adaptive motion planning framework, featuring a dual-triggering mechanism (periodic and safety-driven) and a complete trajectory generation pipeline, which integrates constrained path planning, trajectory parameterization, and trajectory refinement.
Note: All videos are shown at real-time speed (1x) unless otherwise stated.
The proposed trajectory generation method is first evaluated in static simulations. The environments include a narrow passage, a table obstacle, and a cluttered scene. Comprehensive quantitative results are summarized in Table I of the paper.
Our method is better suited for objects exhibiting sufficient inherent stability margins (minimum stability margin, i.e., MSM ≥ 9.5°). The video below showcases the robotic arm counteracting the object's centrifugal motion through wrist rotation under extreme motion aggressiveness.
This section compares the proposed method with a strong reactive baseline adapted from the MPC approach in [1] to demonstrate the necessity of global guidance.
Ours (An open space)
Baseline (An open space)
Ours (A narrow passage)
Baseline (A narrow passage)
Ours (A table obstacle)
Baseline (A table obstacle)
Ours (A cluttered scene)
Baseline (A cluttered scene)
This section evaluates the reactivity of the proposed framework in quasi-static yet intermittently changing environments. The reactive strategies primarily comprise replanning and safe stop planning, as demonstrated below.
The replanning maneuver in response to a sudden obstacle
The safety-stop maneuver in response to a sudden obstacle
We conduct repeated transportation trials to evaluate reactivity across various motion aggressiveness levels and MSMs. The statistical results are summarized in Table II of the paper.
Low aggressiveness,
MSM: 14.0°
Medium aggressiveness,
MSM: 14.0°
High aggressiveness,
MSM: 14.0°
Low aggressiveness,
MSM: 9.5°
Medium aggressiveness,
MSM: 9.5°
High aggressiveness,
MSM: 9.5°
Low aggressiveness,
MSM: 7.1°
Medium aggressiveness,
MSM: 7.1°
High aggressiveness,
MSM: 7.1°
Beyond point-to-point trials, we perform continuous transportation tasks in cluttered and intermittently changing environments to evaluate sustained reactivity.
Since the trajectory optimization depends solely on the transported object's CoM position, this section investigates the system's sensitivity to positional uncertainty under varying levels of aggressiveness to identify practical performance boundaries. The experimental setup is illustrated in the following figure and videos. Quantitative experimental results are summarized in Table II of the paper.
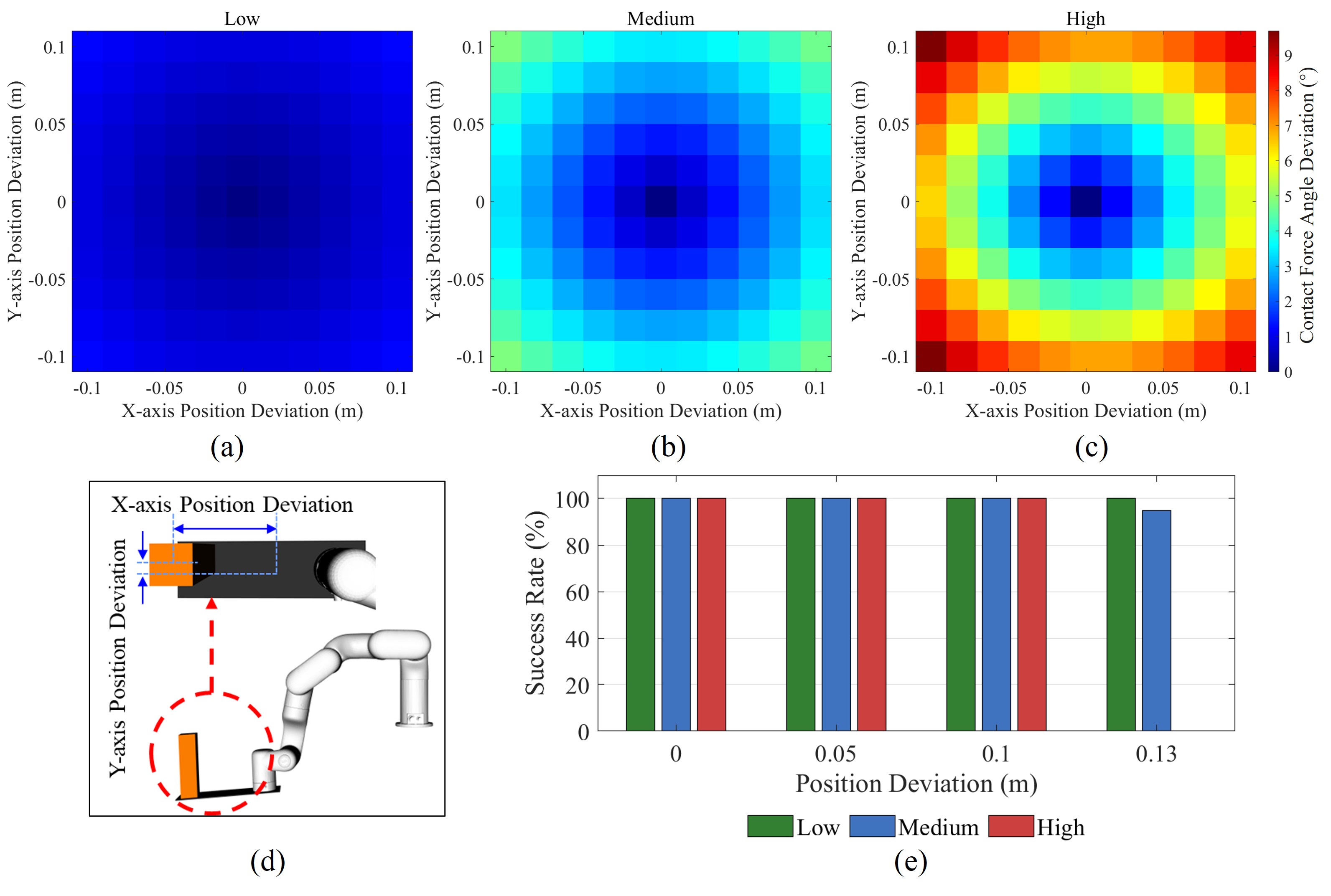
Fig. 3. Illustration of the nominal CoM and the actual CoM offset.
High aggressiveness,
CoM offset: (△x = 0.0 cm, △z = 0.0 cm)

High aggressiveness,
CoM offset: (△x = 10 cm, △z = 0.0 cm)
The proposed method is further validated through a series of real-world experiments. We begin by assessing success rates across varying MSMs and varying levels of motion aggressiveness. (The following videos are shown at 4x speed.)
Low aggressiveness,
MSM: 9.5°
Medium aggressiveness,
MSM: 9.5°
High aggressiveness,
MSM: 9.5°
Low aggressiveness,
MSM: 7.1°
Medium aggressiveness,
MSM: 7.1°
High aggressiveness,
MSM: 7.1°
Low aggressiveness,
MSM: 5.7°
Medium aggressiveness,
MSM: 5.7°
High aggressiveness,
MSM: 5.7°
Low aggressiveness,
MSM: 4.8°
Medium aggressiveness,
MSM: 4.8°
High aggressiveness,
MSM: 4.8°
To further evaluate reactivity and adaptability, we conducted non-prehensile transport of diverse daily objects, including a slender bottle (high tipping risk), milk cartons, and a partially filled water cup. Notably, the implementation relies uniformly on a coarse generic CoM estimate without object-specific parameter tuning.
Transport a slender bottle
Transport milk cartons
Transport a partially filled cup of water
Non-prehensile transportation with frequently changing goal points
To demonstrate the versatility and hardware-agnostic nature of our framework, we conducted further experiments on a Rokae XMate CR20 robotic arm. The results show that our method can be readily applied to different hardware with minimal adaptation.
Non-prehensile transportation in extremely cluttered environments
Transport two slender water bottles
Transport three slender water bottles
Transport two objects stacked vertically (front view)
Transport two objects stacked vertically (side view)
This letter proposes a reactive motion planning framework, enabling non-prehensile transportation in cluttered, quasi-static yet intermittently changing environments. Compared to purely reactive SOTA methods, our approach leverages global geometric guidance to effectively circumvent local minima. By employing simplified contact constraints and a hierarchical architecture, our method reduces the computation time for long-horizon trajectory generation from the scale of seconds to the hundred-millisecond range. Furthermore, the performance boundaries resulting from this simplification are rigorously evaluated through extensive experiments. Future work will focus on addressing the aforementioned limitations and enhancing safety while maintaining computational efficiency.